テニスの最適なサーブ確率
テニスはサーブを二回打つことが出来るスポーツです。1stサーブが入らなくとも2ndサーブを打つ権利があります。
このことから、「1stサーブは攻撃的に打つべし、2ndサーブは安全に打つべし」ということが一般的に言われていますし、直観にも反していない考え方です。
では、どの程度攻撃的に1stサーブを打てば良いのでしょうか?また、どの程度安全に2ndサーブを打てば良いのでしょうか?
ここでは、それらをある程度定量的に評価したいと思います。
ポイント獲得率
僕らの目的は最終的にポイントを取ることですから、ポイントを取れる確率を最大化しましょう。
そのためにポイント獲得率を評価してみます。
\(n\)-thサーブが入る確率を\(p_n\), \(n\)-thサーブが入ったあとに得点出来る確率を\(q_n\)とします(\(n=1,2\))。
よくテレビ中継で、各選手のスタッツが評価されますが、そこで使われる用語を使うと、
\(p_1\)は1st serve %, \(p_2\)は2nd serve %,
\(q_1\)は1st serve Points won, \(q_2\)は2nd serve Points wonです。
このとき、ポイントを取れる確率\(Q\)は、
\[
Q=p_1 q_1 + (1-p_1)p_2 q_2\ ,
\]
で与えられます。ここで、\(p_n q_n\)は\(n\)-thサーブが成功して、かつその後のラリーも含めて得点出来る確率です。
1stサーブが入らなかった場合のみ2ndサーブを打ちますから第二項の前には、\(1-p_1\)が掛かっています。
ここで注意して欲しいのは\(q\)は独立ではなく\(p\)に依存するということです。(ここから特に混乱がない限り、しばしば添え字の1,2は省略します。)
例えば、攻撃的なサーブを打つと\(p\)は下がりますが、そのあとのラリーが有利になるので\(q\)は上がるでしょう。
つまり\(q\)は\(p\)の関数ですから、サーブが入ってしかも得点出来る確率をまとめて、
\[
f(p)=pq\ ,
\]
と書くことにしましょう。\(f(p)\)の関数形を想像すると、おそらくした図のようになると思われます。
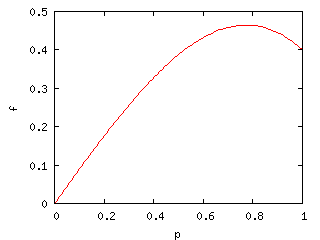
もしサーブが入る確率が0なら、絶対にポイントできませんから、\(f(p=0)=0\)です。
一方、サーブを超確実に(例えばアンダーサーブで)打っても、ポイントできる可能性はありますのでグラフの右端では有限の値になります。
おそらく、いい塩梅の確率でサーブを打ったときに、\(f\)は最大になりますから、まあ大体こんな感じのグラフになるのではないでしょうか。
ポイント獲得率\(Q\)は今定義した関数\(f(p)\)を使って書くと、
\[
Q(p_1,p_2)=f(p_1)+(1-p_1)f(p_2)\ ,
\tag{1}
\label{Q}
\]
となります。ここで、\(Q\)が\(p_1\)と\(p_2\)のみの関数であることを明示するために引数を明示しました。
続くセクションでは、どのように\(p_1\), \(p_2\)を選べば\(Q\)を最大化できるかを考えていきます。
最適な2ndサーブ確率
式(\ref{Q})から、最適な2ndサーブの確率はすぐ分かります。\(p_2\)は第二項の\(f\)の中にしかありませんし、その係数は\(1-p_1\)で正になっています。
よって、\(p_2\)は\(f(p_2)\)を最大化するように選べばよいことが分かります。上の図でいえば最大値のところです。
つまり、2ndサーブを打つことになったら、そこでポイントを取れる確率を最大化すればよいということです。
これはほぼ自明なことを言っていますが、意外と忘れていることかもしれません。
2ndサーブは自分のサーブの中で最も得点率が高いものを選択しなければいけません。
入る確率が最も高いサーブを選んではいけません。
これもまたよく考えれば自明なのですが、
1stサーブでの得点率(サーブが入ってかつ得点出来る確率)は、2ndサーブのそれよりも低くなければなりません。
2ndサーブの得点率の方が低い人は、2ndも1stと同じように打った方が得します。
「1stサーブ攻撃的に打つべし」の証明
前のセクションで、2ndサーブは\(f\)を最大化するように選べばよいことが分かりました。
よって、\(p=p_m\)のときに\(f\)が最大値\(f_m\)をとるとすると、\(Q\)は、
\[
Q(p_1)=f(p_1)+(1-p_1)f_m
\tag{2}
\label{Q2}
\]
となります。この関数を最大化する\(p_1\)が最適な1stサーブ確率です。
しかし、\(f(p)\)の具体的な関数形が分かっていないので、これ以上なんとも言えません。
そこで、最もらしい仮定を置きましょう。\(f(p)\)は\(p=p_m\)の近傍では十分滑らかであるとします。
このとき、\(p_1=p_m+\delta p\) (\(\delta p \ll 1\))とおくと、
\[
f(p_1)\simeq f_m+\frac{1}{2}f''(p_m)\delta p^2\ ,
\]
のように近似できます。\(f\)は\(p=p_m\)で最大値を取りますから、\(\delta p\)の一次の項はありません。
また、\(f''(p_m)<0\)であることにも注意してください。この近似を使うと、
\[
Q(p_1)\simeq f_m+(1-p_m)f_m - f_m \delta p - \frac{1}{2}|f''(p_m)| \delta p^2=Q(p_m)- f_m \delta p - \frac{1}{2}|f''(p_m)| \delta p^2
\ ,
\tag{3}
\label{Qap}
\]
が得られます。ここから分かることは\(\delta p < 0\)にすると、\(Q(p_1)>Q(p_m)\)になるので得になります。
一方、\(\delta p > 0\)にすると損をします。
よって、1stサーブ成功率は2ndサーブ成功率よりも(少なくとも微小に)低い方が有利であるという結論が得られます。
これにより、一般に言われている「1stサーブは攻撃的に打つべし」の証明が得られました。
\(f(p_1)\)を多少犠牲にしてでも、\(q_1\)を上げた方が得ということですね。失敗してももう一回打てるのですから。
最適な1stサーブ確率
もう少し\(f(p)\)の形を具体的に仮定して最適な1stサーブ確率を調べてみましょう。
そのために、より想像しやすい\(q(p)\)の関数形が大体どうなるかをまず考えてみます。
サーブを攻撃的にすればするほど、(もしそれが入れば)得点率は増大するでしょう。つまり、\(q\)は\(p\)の単調減少関数になるということです。
しかし、人間の筋力に限界はありますから、サーブ確率を下げても得点率はそのうち頭打ちになるはずです。よって、大ざっぱに\(q(p)\)の関数形を想像すると下図のようになりそうです。
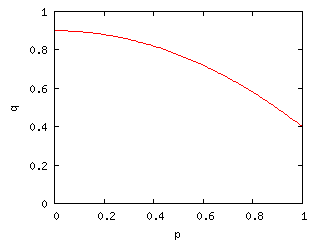
このような関数形なら大体二次関数で近似できそうです。そこで、
\[
q(p)=a(-p^2+b)\ ,
\]
と置いてみます。ここで、\(a,b\)は定数です。このとき\(f\)は、\(f(p)=ap(-p^2+b)\)
となります。今、\(p=p_m\)のときに\(f\)が最大値をとるとしているので、\(f'(p_m)=0\)より\(a=f_m/(2p_m^2), b=3p_m^2\)となります。
結局\(f\)は、
\[
f(p)=\frac{f_m}{2p_m^2}p(-p^2+3p_m^2)
\]
と書けることになります。このとき、トータルのポイント獲得率(\ref{Q2})は、
\[
Q(p_1)= \left[\frac{1}{2p_m^2}p_1(-p_1^2+3p_m^2)+(1-p_1)\right]f_m\ ,
\]
です。これを最大化する、\(p_1\)を探せばよいわけですから、\(Q'(p_1)=0\)より最適な1stサーブの確率は、
\[
p_1=\frac{p_m}{3}\sqrt{9-6p_m}\ ,
\]
となります。\(p_m\),つまり,2ndサーブが分かれば、1stサーブの最適な確率が分かります。
しかし、ほとんどの人にとってはこれをわざわざ計算する必要はありません。というのも、上式を
\(1-p_m\)でテーラー展開してやると、
\[
p_1=\frac{1}{\sqrt{3}}-\frac{1}{2\sqrt{3}}(1-p_m)^2+\cdots\ ,
\]
となります。ほとんどの人は\(p_m\)は1の近いはずなので、上式のleading orderだけ見れば十分でしょう。
よって、最適な1stサーブ確率は普遍的に
\[
p_1\simeq \frac{1}{\sqrt{3}}\ ,
\]
で与えられます。つまり、\(q(p)\)が二次関数で与えられることを信じるのであれば最適な1stサーブ確率は、ほとんど誰にとっても約58%となります。
まとめと考察
最終的にポイントが取れる確率を最大化することで、最適な1stサーブ,2ndサーブの確率を評価しました。
その結果、
- 2ndサーブは自分のサーブの中で最も得点率が高いものを選択する。
- 1stサーブ確率は2ndサーブの確率よりも、(少なくとも微小に)低くした方が得である。
- 2次関数モデルを用いると、最適な1stサーブ確率は約58%である。
であることが分かりました。これらの結論は、どの程度現実のテニスを表すでしょうか?
これらの結論を導くのに用いた仮定が正しいかどうかが問題です。
1は何も仮定せずに導けます。よって、これはテニスにおける真理です。
2はどうでしょうか?ここでは、関数\(f(p)\)が、最大値と取る点の周りでなめらかであることを仮定しました。
もし、最大値で上に尖った関数形(微分が不連続)をしていたら、2は成り立たなくなります。
しかし、関数が最大値あたりでたまたま特異になっているというのも変な気はします。
実際テニスのプロも1stの方が確率は低くなっていますし、まあ正しそうです。
3はどうでしょうか?これを導くにあたり、すこし大胆ですが\(q(p)\)が二次関数であることを仮定しました。
おそらく誰も\(q(p)\)を評価した人はいないでしょうから、この仮定が正しいかどうかはよく分かりません。
でも、プロの試合を見てると1stサーブ確率は50〜70%
位なので、我々の結果58%
はまあまあいい線を言ってると思います。
少なくとも、最適サーブ確率を計算する定性的なモデルであると言ってもよさそうです。

